Layer Normalization
Published:
Layer Normalization is a technique in deep learning that addresses the covariate shift problem by normalizing thanks to the mean and variance calculated across features for each example.
Covariate Shift Covariate shift occurs when the distribution of variables in the training data is different to real-world or testing data. Therefore, covariate shift can make the model generalize poorly.
While Batch Normalization (BN) is dependent on the mini-batch size ($N$), LayerNorm (LN) normalizes for a single sample across features. Unlike BN, LN does not impose any constraint on the size of a mini-batch and it can be used in the pure online regime with batch size 1. This makes it suitable for Recurrent Neural Networks for example where we have sequential data.
Formula
\[y_i = \gamma \cdot \frac {x_i - \mu} { \sqrt{\sigma ^ 2 + \epsilon}} + \beta\]$\epsilon$ is just put there to avoid cases where the variance is 0.
Let’s see an example.
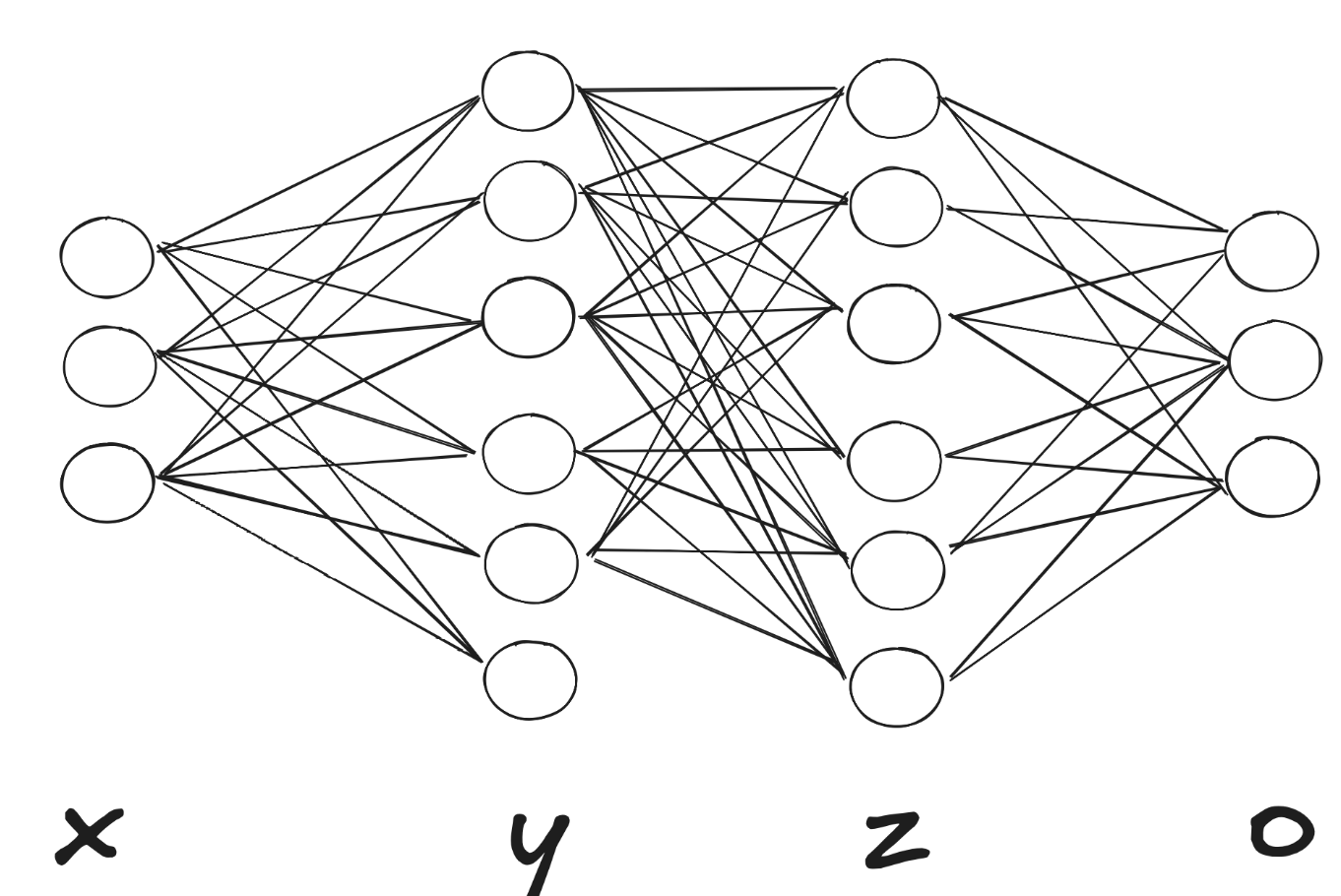
In this set of Neurons, we would at each hidden state (e.g $y$) do the Layer Normalization across all features (neurons) for each individual sample.
Let’s say we start with a batch of $N$ samples, each processed through the network:
The Input layer $x$ consumes an $N\times15$ matrix (e.g. N=100, 15 features), then after the linear + activation in layer $y$, we have an $N\times D_y$ matrix of activations (in the sketch $D_y=6$).
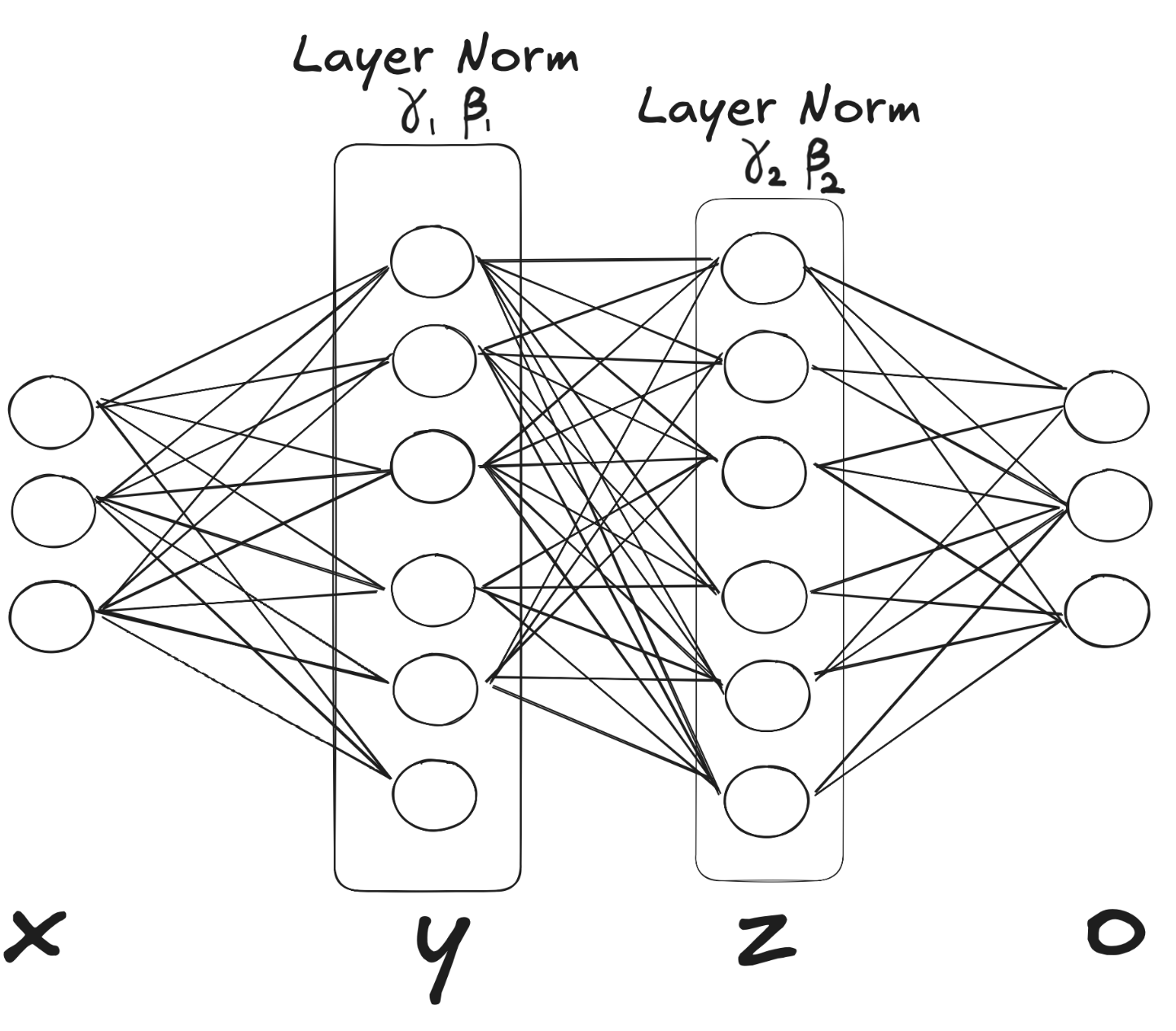
LayerNorm on $y$ sits between $y$ and the next weights. It takes each row (one sample’s 5-vector) and normalizes it to zero mean and unit variance independently of every other sample using the formula we described before.
For each sample $n=1,\dots,N$:
- Compute its mean across the $D_y$ features: $\displaystyle \mu_n = \frac1{D_y}\sum_{i=1}^{D_y} Y_{n,i}.$
- Compute its variance:
$\displaystyle \sigma_n^2 = \frac1{D_y}\sum_{i=1}^{D_y}(Y_{n,i}-\mu_n)^2$ - Normalize & scale each feature i: $\widehat Y_{n,i} = \frac{Y_{n,i}-\mu_n}{\sqrt{\sigma_n^2 + \varepsilon}}$
Then it applies a learned per-feature scale ($\gamma_1$) and shift ($\beta_1$), giving a new $N\times D_y$ that is ready to feed into layer $z$. Similarly for layer $z$, you start with the $N\times D_y$ output of $y$ and apply LayerNorm with its own $\gamma_2,\beta_2$ across each row (for $n$ in $N$)

Comments